
Tessellattions with pentagons
by Albert Gübeli
Introduction
As an enthusiastic reader of Martin Gardners column “Mathematical Games” in the Scientific American during the seventys and eightys, I was especially fond of the article “Extraordinary nonperiodic tiling that enriches the theory of tiles” on January 1977. Due to this article I invented the Pentalbi Legestein (Schweizerische Eidgenossenschaft Patentschrift 615593 15.12.1980).
Pentalbi
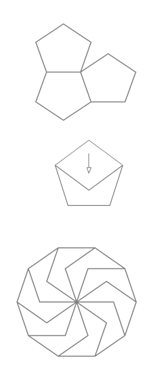
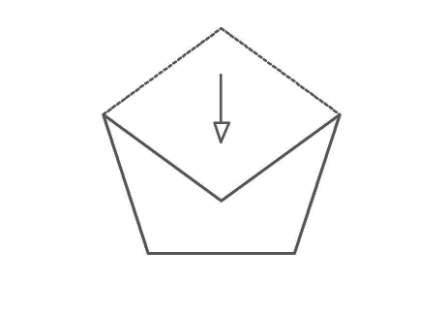
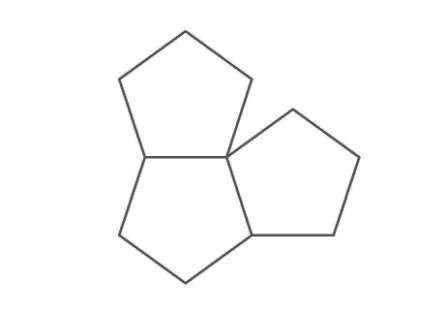
Shapes that fit together without overlapping or living gaps are said to tessellate. It is impossible to tessellate with regular pentagons. With a small trick, you turn two sides of the pentagon and you get new pieces named Pentalbi Legesteine (folded pentagons) and then tessellating in nearly endless combinations becomes possible. Some of the unimaginable possibilities of fascinating figures with only 7 pieces are shown in the following pictures.

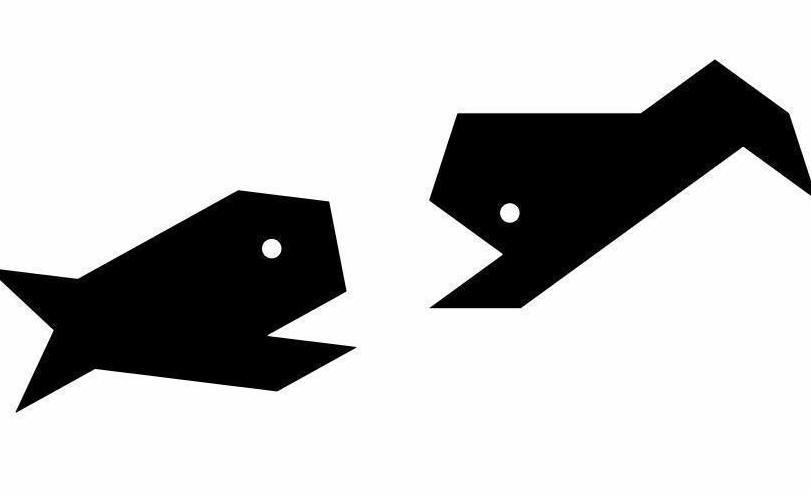


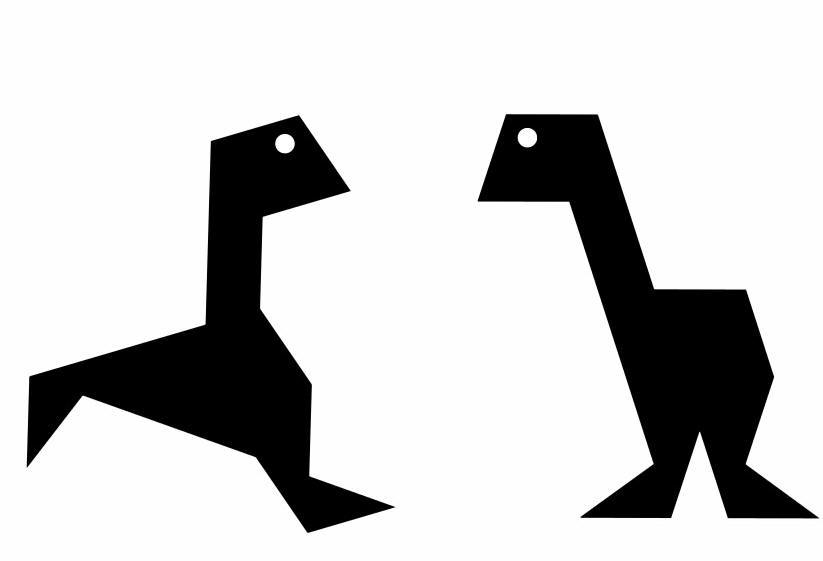
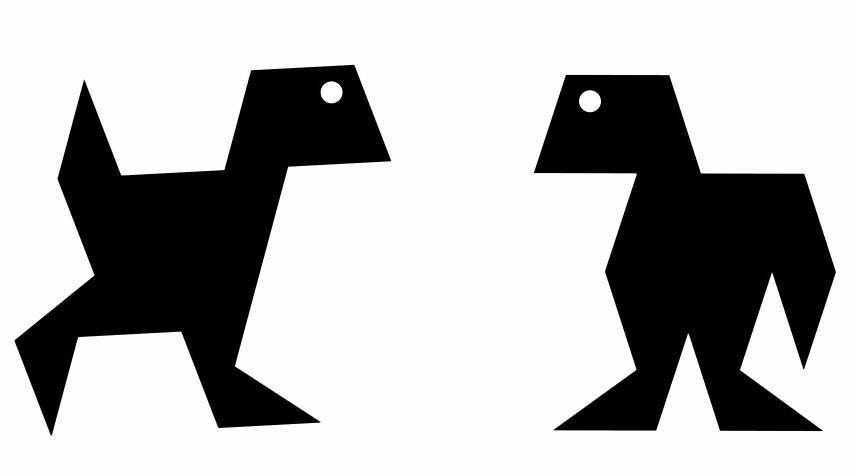
Jeannes Fabelwesen (Jeannes fable beings)
When the straight sides from the Pentalbi pieces are replaced by double circle lines as shown, you get a new exciting puzzle piece that doubles the possibilities of combinations.
The piece is loosing its symmetry, when you turn it backside up you get the mirror image but the piece is no more congruent.
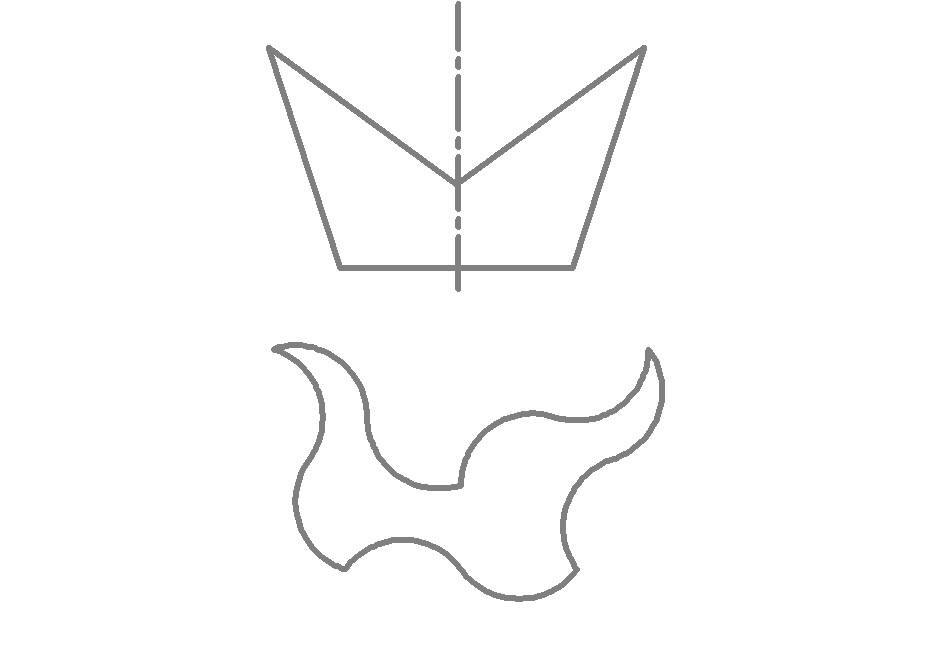
The next picture shows the 24 possible combinations for 2 pieces with at least one common double circle line.


The tricky thing is, that you can tessellate in the right-handed system or in the mirror left-handed system, but not in both!
The basic idée with “Jeannes Fabelwesen” is to explore and create you own new figures.
Naturally you can also copy the patterns how is not so easy how it looks.
You can form new units with 2 or more pieces and then explore a new wonderful world of "Jeannes Fabelwesen". The picture shows examples with 2 and 4 piece units.
Pentalbi was produced under license from 1978 -1986 by NAEF Spiele in Switzerland, and from 2004 by the author.
Jeannes Fabelwesen is produced since 2005 by the author.
The last picture shows a nonperiodic tiling.
